Trigonometric Functions in Excel: 10 Essential Formulas with Examples & Free Templates

Meta Description :

Trigonometric functions in Excel are essential tools for performing complex mathematical and scientific calculations. Whether you’re working on engineering projects, data analysis, or academic tasks, mastering these functions can save you time and improve accuracy. In this guide, we’ll explore how to use trigonometric functions in Excel, including SIN, COS, and TAN, with practical examples and free downloadable templates

Section 1 : What Are Trigonometric Functions in Excel?
« Trigonometric functions in Excel allow you to perform calculations based on angles and triangles. These functions, such as SIN, COS, and TAN, are widely used in fields like engineering, physics, and finance. By understanding how to use trigonometric functions in Excel, you can solve problems more efficiently and create dynamic models. »

Section 2 : Practical Examples of Trigonometric Functions in Excel
« Let’s dive into some practical examples of trigonometric functions in Excel. For instance, you can use the SIN function to calculate the sine of an angle, the COS function for cosine, and the TAN function for tangent. These examples will help you apply trigonometric functions in Excel to real-world scenarios.

Common Trigonometric Functions: SIN, COS, TAN

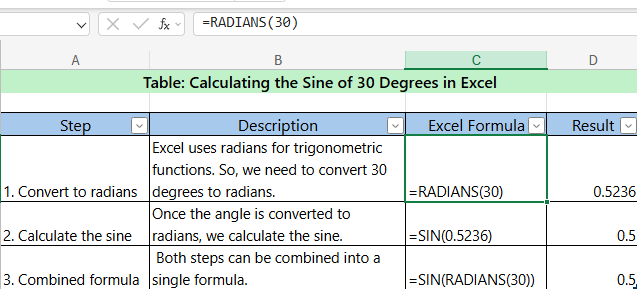
1. SIN (Sine) How to use the SIN function in Excel

• Description : Calculates the sine of an angle.
• Syntax : =SIN(angle)
• Example : Calculate the sine of 30 degrees.
• =SIN(RADIANS(30)) // Result : 0.5

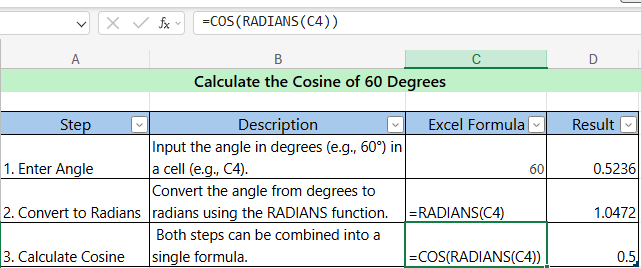
2. COS (Cosine) Convert degrees to radians in Excel

• Description : Calculates the cosine of an angle.
• Syntax : =COS(angle)
• Example : Calculate the cosine of 60 degrees. =COS(RADIANS(60)) // Result : 0.5

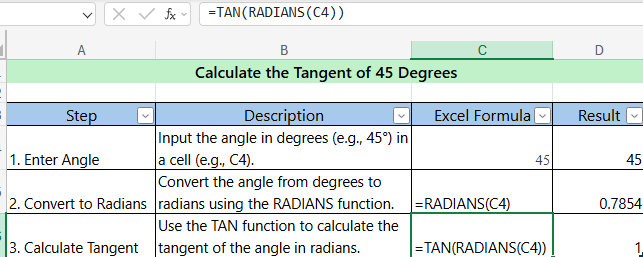
3. TAN (Tangent)

• Description : Calculates the tangent of an angle.
• Syntax : =TAN(angle)
• Example : Calculate the tangent of 45 degrees. =TAN(RADIANS(45)) // Result : 1

4. ASIN (Arc Sine)

• Description : Calculates the angle from a sine value.
• Syntax : =ASIN(value)
• Example : Find the angle whose sine is 0.5. =DEGREES(ASIN(0.5)) // Result : 30 degrees

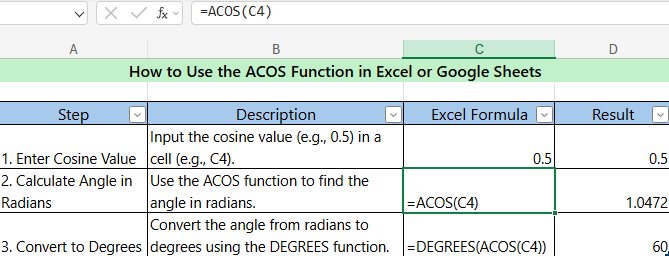
5. ACOS (Arc Cosine)

• Description : Calculates the angle from a cosine value.
• Syntax : =ACOS(value)
• Example : Find the angle whose cosine is 0.5. =DEGREES(ACOS(0.5)) // Result : 60 degrees

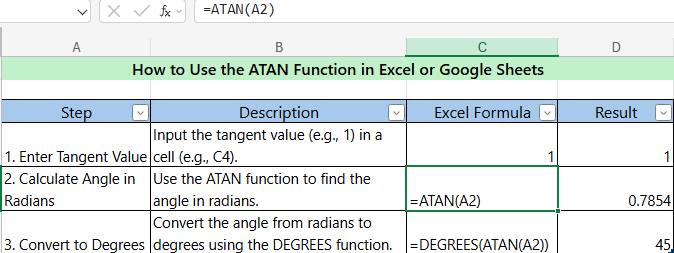
6. ATAN (Arc Tangent)

• Description : Calculates the angle from a tangent value.
• Syntax : =ATAN(value)
• Example : Find the angle whose tangent is 1. =DEGREES(ATAN(1)) // Result : 45 degrees

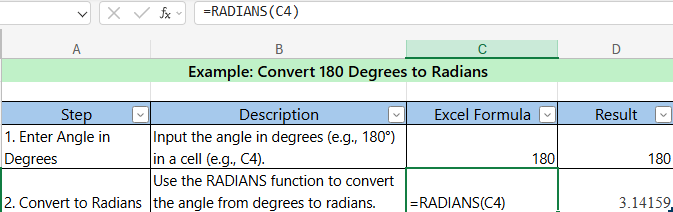
7. RADIANS (Convert to Radians)

• Description : Converts an angle from degrees to radians.
• Syntax : =RADIANS(angle)
• Example : Convert 180 degrees to radians. =RADIANS(180)) // Result : 3.14159 (π)

8. DEGREES (Convert to Degrees)

• Description : Converts an angle from radians to degrees.
• Syntax : =DEGREES(angle)
• Example : Convert π radians to degrees. =DEGREES(PI())) // Result : 180 degrees

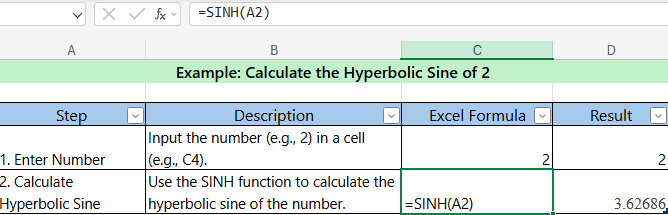
9. SINH (Hyperbolic Sine)

• Description : Calculates the hyperbolic sine of a number.
• Syntax : =SINH(number)
• Example : Calculate the hyperbolic sine of 2. =SINH(2)) // Result : 3.62686

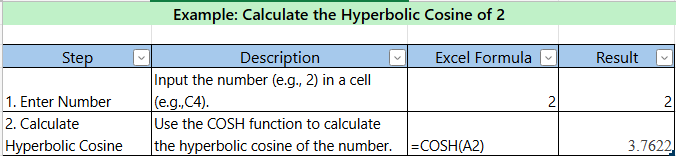
10. COSH (Hyperbolic Cosine)

• Description : Calculates the hyperbolic cosine of a number.
• Syntax : =COSH(number)
• Example : Calculate the hyperbolic cosine of 2. =COSH(2)) // Result : 3.76220

Advanced Applications of Trigonometric Functions in Excel 1. Calculating the Height of a Right Triangle Using SIN: A Visual Approach –Free Excel templates for trigonometry

Context:
Beyond the classic calculation of the height of a right triangle, you can use Excel to create an interactive tool that visualizes how the height changes based on the angle or hypotenuse.

Innovative Steps:

1. Dynamic Table:
   • Create a table where the user can input the hypotenuse and angle.
   • Use the formula =Hypotenuse * SIN(RADIANS(angle)) to calculate the height.
   • Add a real-time graph that updates the height as values change.
2. Data Validation:
   • Limit the angle to a range of 0° to 90° to avoid inconsistent results.
   • Use the formula =IF(angle > 90, "Invalid angle", Hypotenuse * SIN(RADIANS(angle))) to display an error message.
3. Practical Application:
   • Imagine a scenario where you need to calculate the height of a ladder leaning against a wall. The Excel tool allows you to test different angles to optimize stability.

Excel File:
Download an interactive template where you can adjust the hypotenuse and angle to see the height update automatically.

2. Modeling a Sine Wave: Adding Realism with Variable Parameters

Context:
Sine wave modeling is often taught in a static manner. However, in practice, waves have variable amplitudes, frequencies, and phases. Create a dynamic Excel model to simulate realistic waves.

Innovative Steps:

1. Variable Parameters:
   • Add sliders (scroll bars) to adjust amplitude, frequency, and phase in real time.
   • Use the formula =Amplitude * SIN(2 * PI() * Frequency * Time + RADIANS(Phase)).
2. Advanced Visualization:
   • Overlay multiple waves to study interference.
   • Add an option to display the wave in degrees or radians.
3. Practical Application:
   • Simulate sound or light signals for scientific or educational projects.
   • Study the effect of phase on wave superposition.

Excel File:
Download an interactive template with sliders to adjust wave parameters.

3. Degrees/Radians Conversion: Automation for Large Data Sets

Context:
Converting between degrees and radians is often tedious, especially for large data sets. Automate this process using advanced Excel techniques.

Innovative Steps:

1. Dynamic Table:
   • Import a CSV file containing angles in degrees.
   • Use the formula =RADIANS(angle) to convert to radians.
   • Add a verification column with =DEGREES(angle_in_radians).
2. Macro for Automation:
   • Record a macro to automatically convert thousands of angles with a few clicks.
   • Add a button in Excel to run the macro.
3. Practical Application:
   • Process astronomical data (star positions) or engineering angle measurements.
   • Generate automated reports with converted angles.

4. Creative Applications of SIN in Everyday Life

Context:
The SIN function is not limited to pure mathematics. Here are some innovative ideas for using it in practical projects:

1. Designing an Access Ramp:
   • Calculate the optimal slope for an access ramp based on the angle and height.
   • Use the formula =Height / SIN(RADIANS(angle)) to determine the ramp length.
2. Lighting Optimization:
   • Model the angle of light incidence to maximize natural lighting in a room.
   • Use SIN to calculate light intensity based on the sun’s angle.
3. Simulating Periodic Motion:
   • Create models to simulate movements like pendulum oscillations or waves.

Conclusion:

In conclusion, Excel’s trigonometric functions—such as SIN, COS, TAN, and more—are indispensable tools for performing accurate mathematical and scientific calculations. Whether you’re a student, engineer, data analyst, or simply looking to enhance your Excel skills, mastering these functions can significantly improve your efficiency and precision. This guide has provided you with a clear understanding of how to use these functions, along with practical examples to help you apply them in real-world scenarios.

To further support your learning, we’ve included downloadable Excel templates (both internal and external models) that you can use to practice and explore these concepts at your own pace. By leveraging these resources, you’ll be well-equipped to tackle complex calculations and unlock the full potential of Excel for trigonometric applications.

Ready to get started? Download this guide here: Download the guide here

Explore additional Excel formulas and resources: Master VLOOKUP in Excel (Free Download)

Visit our website to discover more tools and templates to master Excel:

• Downloadable Excel templates
• Excel for mathematical calculations
• Advanced Excel functions
• Excel for engineers and analysts
• Free Excel practice files

Start exploring today and take your data analysis skills to the next level!